I thought I would share a little of my design process for the LCR filter I am going to insert inline with this loudspeaker in order to smooth out the midrange response to be balanced with the bass and improve the apparent treble to some degree.
Note that this speaker has a baffle size of 10-1/4 by 8-1/2 inches. That means the baffle step loading will start to drop at about 400Hz and reach a full 6dB drop by 330Hz. The math for determining this is: Speed of Sound divided by Length divided by Four. The speed of sound in inches is 13,536 inches per second. The short length is 8.5 inches. So, 13,536 / 8.5 / 4 = 398Hz. the long length math is 13,536 / 10.25 / 4 = 330Hz. That is not complicated math, is it?
So, I knew the filter would have to start having an impact on the electrical signal going to the speaker starting at approximately 300Hz. Since the treble starts rolling off significantly at about 5,000Hz, so I wanted to end the influence of the filter at about 5,000Hz so the signal above that frequency is not reduced.
Rather than relying on the math to determine the ideal filter, I performed measurements from the location of my head while seated at my desk in front of the speakers. The goal is to get the best sound in this real world location, not in an anechoic chamber. I input the measurements I made of both the acoustical frequency response and acoustic phase response as well as measurements of the electrical impedance and electrical phase into a crossover modelling program I own and created a virtual filter based on the math then adjusted the values of the resistor, inductor and capacitor to get the best results for my actual real-life system.
After fidgeting with the values and settling on something I think will work well, the finished filter I am going to make looks like this:
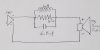
As shown in the diagram, the positive signal has the filter inserted inline. The inductor determines at which low frequency the electrical signal will be reduced as the frequency raises. The capacitor determines at which high frequency the electrical signal will stop being reduced as the frequency raises. The resistor determines how much cut in level the filter will peak at the center of the operating range. All three interact with one another, so changing the value of any single component will alter the resulting performance of the others to some extent. So, having a modeling program is essential to the design process. In the olden days before simple crossover simulators existed, I would calculate using lots of paper, equations from a filter design book, and a proper electronic calculator to estimate the ideal values. Then I would assemble a test filter and measure the results electronically and acoustically, which also meant plotting values on logarithmic graph paper. Then I would alter the filter to adjust for real world results until I got the performance I was seeking. I got pretty good at testing up to 6 variants of a filter in one day using that method - and I thought I was fast!
Anyway, in addition to the components of the filters impacting one another, the impedance of the loudspeaker is also not linear. That means that how the filter would operate if the speaker were a perfect resistive load of 8 ohms (which is how the manual equations are written), the actual impedance of the speaker is reactive and thus the performance will vary. At a test voltage of 1V, the resistance of this particular driver at 300Hz is 7.53 Ohms, but it rises to a resistance at 5,000Hz of 11.9 Ohms. So, a capacitor calculated to be a certain value based on an 8 Ohm load will not start to impact the signal at 5,000Hz. Keep in mind, the impedance changes with input voltage, as well, because heat and the voice coil's position in the magnetic gap also cause variation in the resistance at various frequencies. These variations in impedance based on voltage and the reactive nature of the driver itself are major contributors to why I heavily recommend active crossovers and the complete removal of any passive components in a crossover/filter.















